サポートベクターマシン（SVM）完全解説：機械学習の強力な分類器を理解する

サポートベクターマシン（Support Vector Machine、SVM）は、機械学習の中でも特に強力で理論的に美しいアルゴリズムの一つです。

画像認識、テキスト分類、医療診断など、様々な分野で高い性能を発揮し、深層学習が台頭する前は「最強の分類器」として君臨していました。この記事では、SVMの基本原理から実装まで、初心者にも分かりやすく解説します。

目次

  1. SVMとは？
  2. SVMの基本原理
  3. 線形SVMと非線形SVM
  4. カーネルトリック
  5. ハイパーパラメータC
  6. Pythonでの実装
  7. SVMの長所と短所
  8. まとめ

SVMとは？

サポートベクターマシン（SVM）は、データを2つのグループに分類するための教師あり学習アルゴリズムです。

SVMの核心アイデア

「データを分ける境界線を引くなら、できるだけ余裕を持った境界線を引こう」

これがSVMの基本思想です。単にデータを分けるだけでなく、マージン（余白）が最大になる境界線を見つけることで、新しいデータに対しても頑健な分類を実現します。

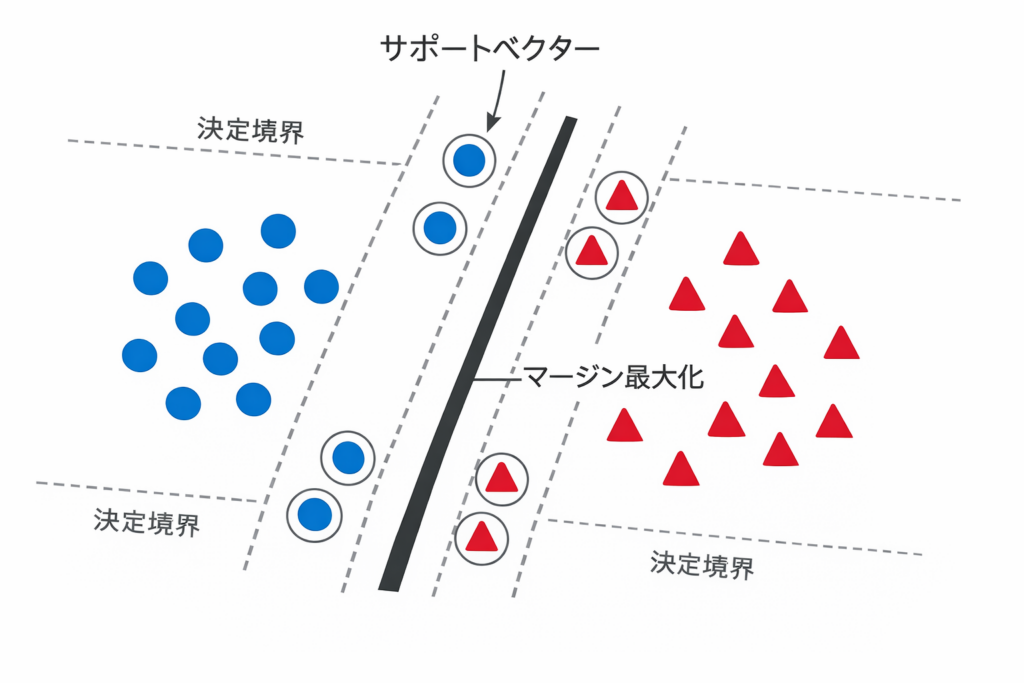
SVMの基本原理

1. 決定境界とマージン

SVMは以下の要素で構成されます：

要素説明
決定境界データを2つのクラスに分ける線（または平面）
マージン決定境界から最も近いデータ点までの距離
サポートベクターマージンの境界線上にあるデータ点

2. マージン最大化

SVMの目的はマージンを最大化することです。

目的関数：マージンを最大化
制約条件：すべてのデータを正しく分類

数式で表すと：

最大化:2‖w‖最大化 : \\\\\frac{2}{\|w\|}
制約:yi(w⋅xi+b)≥1(∀i) 制約 : y_i ( w \cdot x_i + b ) \ge 1 \quad (\forall i)
  • w: 決定境界の重みベクトル
  • b: バイアス（切片）
  • y_i: データのラベル（+1 or -1）
  • x_i: データ点

3. なぜマージンが重要か？

マージン分類性能
狭い訓練データには正確だが、新データには弱い（過学習）
広い新しいデータにも頑健（汎化性能が高い）

🤖 AIの世界では：
マージンが広い = 「ちょっとした誤差があっても大丈夫」という余裕を持った判断ができるということです。これが、SVMが実世界のノイズの多いデータでも高性能を発揮する理由です。

線形SVMと非線形SVM

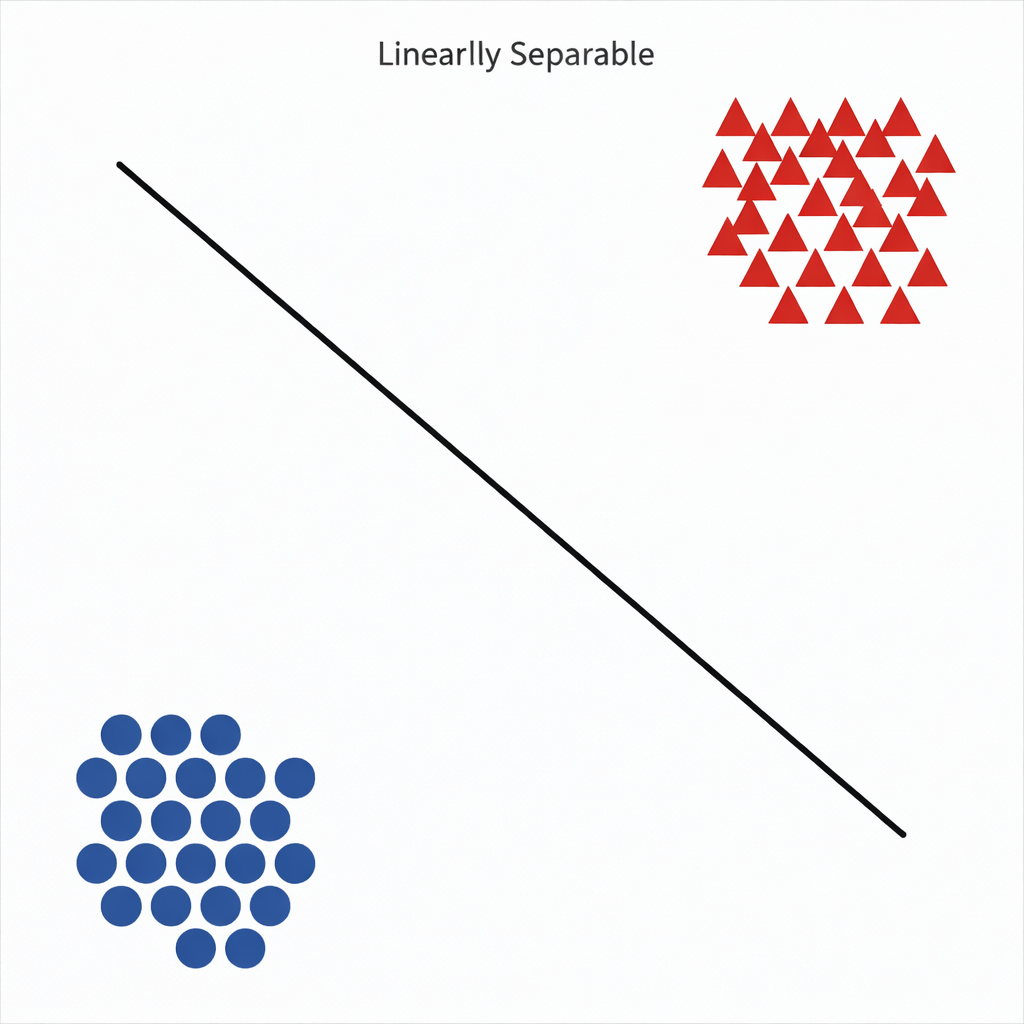
線形SVM（Linear SVM）

データが直線（または平面）で分離できる場合に使用します。

from sklearn.svm import SVC
import numpy as np

# 線形分離可能なデータ
X = np.array([[1, 2], [2, 3], [3, 3], [6, 5], [7, 7], [8, 6]])
y = np.array([0, 0, 0, 1, 1, 1])

# 線形SVM
model = SVC(kernel='linear')
model.fit(X, y)

# 予測
new_point = np.array([[5, 4]])
print(model.predict(new_point))  # 0 or 1
Python

非線形SVM（Non-linear SVM）

データが直線では分離できない場合、カーネルトリックを使って高次元空間に変換します。

カーネルトリック

カーネルトリックは、データを高次元空間に写像することで、複雑な境界を直線（平面）で表現する技術です。

主要なカーネル関数

カーネル数式特徴用途
線形K(x, x') = x・x'最もシンプル線形分離可能なデータ
多項式K(x, x') = (γx・x' + r)^d曲線的な境界中程度の複雑さ
RBF（ガウシアン）`K(x, x’) = exp(-γx-x’
シグモイドK(x, x') = tanh(γx・x' + r)ニューラルネット風特殊な用途

カーネルの選び方

判断フロー：
1. まず線形カーネルを試す → ダメなら
2. RBFカーネルを試す → それでもダメなら
3. 多項式カーネルを試す

最も一般的なのはRBF（Radial Basis Function）カーネルです。

# RBFカーネルSVM
model = SVC(kernel='rbf', gamma='scale')
model.fit(X, y)
Python

ハイパーパラメータC（より詳しい解説）

Cとは何を制御しているのか？

C は 「どれくらい誤分類を許すか」 を制御するパラメータです。
数学的には、以下のトレードオフを調整しています。

マージンを広く取りたい
vs
訓練データをできるだけ正確に分類したい

Cパラメータの役割

  • Cが大きい
    • 「1点の誤分類も許したくない」
    • 決定境界はデータにピッタリ沿う
    • ノイズにも過剰反応 → 過学習しやすい
  • Cが小さい
    • 「多少間違ってもいいから、大局的に分けたい」
    • 決定境界はなだらか
    • ノイズに強い → 汎化性能が高い
Cの値マージン誤分類傾向
大きい（C=100）狭い許さない過学習しやすい
小さい（C=0.1）広いある程度許す汎化性能が高い

ソフトマージンとハードマージン

なぜハードマージンは使われない？

理論上は：

「すべての点を完璧に分離する」

しかし現実は：

  • ラベルミス
  • センサノイズ
  • 外れ値

が必ず存在します。

マージンの種類説明Cの値
ハードマージン誤分類を一切許さない非常に大きい
ソフトマージン多少の誤分類を許容適度な値

実世界のデータは完全には分離できないため、ソフトマージンが一般的です。

Pythonでの実装

基本的な使い方

from sklearn.svm import SVC
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# データ生成
X, y = make_classification(n_samples=200, n_features=2, 
                          n_redundant=0, n_informative=2,
                          random_state=42)

# 訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42
)

# SVMモデル作成
model = SVC(kernel='rbf', C=1.0, gamma='scale')
model.fit(X_train, y_train)

# 予測と評価
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"精度: {accuracy:.2f}")
Python

多クラス分類

SVMは本来2クラス専用

SVMは「+1 と -1」を分ける問題として設計されています。

SVMは元々2クラス分類用ですが、One-vs-Rest戦略で多クラスにも対応できます。

# 自動的に多クラス対応
X, y = make_classification(n_samples=300, n_classes=3,
                          n_informative=3, n_redundant=0)

model = SVC(kernel='rbf')
model.fit(X, y)  # 3クラス分類も可能
Python

One-vs-Rest (OvR)

例えば 3クラス (A, B, C) の場合：

  • 分類器1：A vs (B,C)
  • 分類器2：B vs (A,C)
  • 分類器3：C vs (A,B)

→ 計3個のSVMを学習

SVMの長所と短所

✅ 長所

長所説明
🎯 高精度多くのタスクで優れた性能
🛡️ 過学習に強いマージン最大化により汎化性能が高い
📐 高次元データに強い特徴量が多くても動作する
🔧 柔軟性カーネルで様々なパターンに対応
💾 メモリ効率サポートベクターのみ保存すればOK

❌ 短所

短所説明
⏱️ 大規模データに弱い計算量が多い（O(n²～n³)）
🔍 解釈が困難なぜその予測をしたか説明しにくい
⚙️ パラメータ調整が必要C、gamma、kernelの最適値を探す必要
📊 確率出力が苦手クラス確率の推定が不正確

SVMが向いているケース

  • データ量が中規模（数千〜数万サンプル）
  • 特徴量が多い（高次元データ）
  • 精度重視（多少の計算時間は許容）
  • ノイズが多いデータ

SVMが向いていないケース

  • 超大規模データ（数百万サンプル以上）
  • リアルタイム予測が必要
  • モデルの解釈性が最重要
  • 確率的な出力が必要

SVMと他のアルゴリズムの比較

アルゴリズム精度速度解釈性大規模データ
SVM⭐⭐⭐⭐⭐⭐⭐⭐⭐❌
ロジスティック回帰⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐
ランダムフォレスト⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐
ニューラルネット⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐

実践例：手書き数字認識

from sklearn.datasets import load_digits
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report

# 手書き数字データセット（0-9の10クラス）
digits = load_digits()
X, y = digits.data, digits.target

# 訓練・テスト分割
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42
)

# SVMモデル
model = SVC(kernel='rbf', C=10, gamma=0.001)
model.fit(X_train, y_train)

# 評価
y_pred = model.predict(X_test)
print(classification_report(y_test, y_pred))
Python

実行結果（例）：

              precision    recall  f1-score
0                 1.00      0.98      0.99
1                 0.95      0.98      0.97
2                 0.98      0.98      0.98
...
accuracy                           0.97

まとめ

SVMについて重要なポイントをまとめます。

今回のポイント

✅ SVM = マージンを最大化して分類する強力なアルゴリズム
✅ サポートベクター = 決定境界に最も近い重要なデータ点
✅ カーネルトリック = 複雑なパターンを高次元空間で線形分離
✅ Cパラメータ = マージンの広さを制御（小さい=広い、大きい=狭い）
✅ RBFカーネル = 最も汎用的で強力なカーネル
✅ 長所 = 高精度・過学習に強い・高次元データに対応
✅ 短所 = 大規模データに弱い・パラメータ調整が必要

実践のヒント

  1. まず線形カーネルから試す – シンプルで高速
  2. 次にRBFカーネル – 多くの場合これで十分
  3. GridSearchでパラメータ調整 – C と gamma を探索
  4. データの正規化を忘れずに – SVMはスケールに敏感
  5. サンプル数が多い場合は他の手法も検討 – ランダムフォレストなど

さらに学ぶために

  • 理論を深く学ぶ → 凸最適化、ラグランジュ乗数法
  • 実践で試す → Kaggleのコンペティション
  • 発展手法 → ν-SVM、One-Class SVM（異常検知）
  • 他のカーネル → カスタムカーネルの実装

練習問題

以下のコードで、SVMの挙動を体験してみましょう。

from sklearn.datasets import make_moons
from sklearn.svm import SVC
import matplotlib.pyplot as plt

# 三日月型データ（非線形）
X, y = make_moons(n_samples=200, noise=0.2, random_state=42)

# 線形SVMとRBF SVMを比較
models = {
    'Linear': SVC(kernel='linear'),
    'RBF': SVC(kernel='rbf', gamma='scale')
}

for name, model in models.items():
    model.fit(X, y)
    score = model.score(X, y)
    print(f"{name} SVM 精度: {score:.2f}")
Python

チャレンジ問題：
異なるCの値（0.1, 1, 10, 100）で訓練し、決定境界がどう変わるか観察してみましょう！

コメント

タイトルとURLをコピーしました