はじめに
深層学習モデルの訓練において、学習率(Learning Rate)は最も重要なハイパーパラメータの一つです。学習率の設定次第で、モデルの収束速度や最終的な性能が大きく変わります。本記事では、学習率の基本概念から実践的な設定方法まで、包括的に解説します。
学習率とは何か
学習率は、勾配降下法においてパラメータを更新する際の「ステップの大きさ」を制御する値です。ニューラルネットワークの訓練では、損失関数を最小化するために、勾配の逆方向にパラメータを更新します。この更新の際、学習率が小さすぎると学習が遅くなり、大きすぎると最適解を飛び越えてしまう可能性があります。
数式で表すと、パラメータθの更新は以下のようになります:
θ_new = θ_old – η × ∇L(θ)
ここで、ηが学習率、∇L(θ)が損失関数Lの勾配を表します。
学習率の影響
学習率が大きすぎる場合
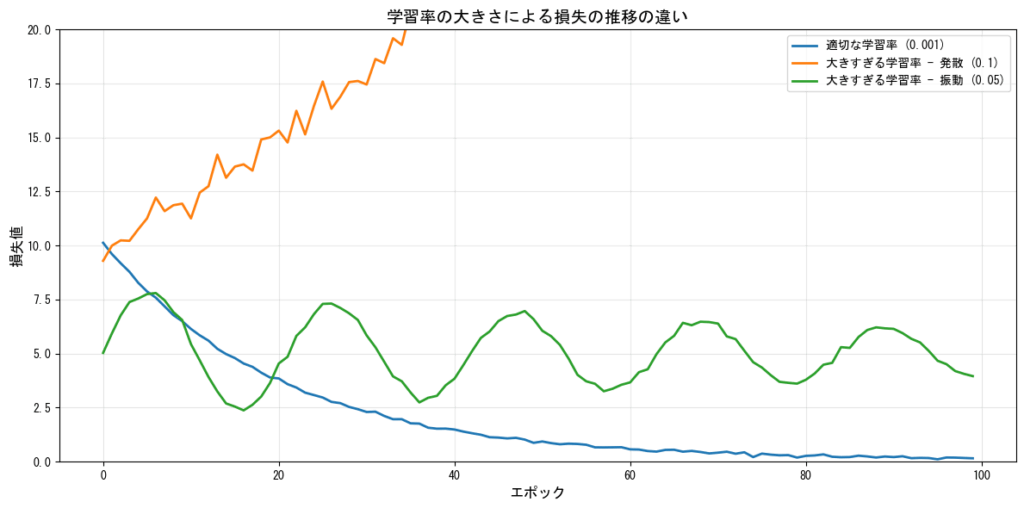
学習率が大きすぎると、以下の問題が発生します:
- 発散(Divergence):損失が増加し続け、学習が失敗する
- 振動(Oscillation):最適解の周辺で振動し、収束しない
- 局所解の飛び越し:良好な解を見つけても、更新が大きすぎて通り過ぎてしまう
学習率が小さすぎる場合
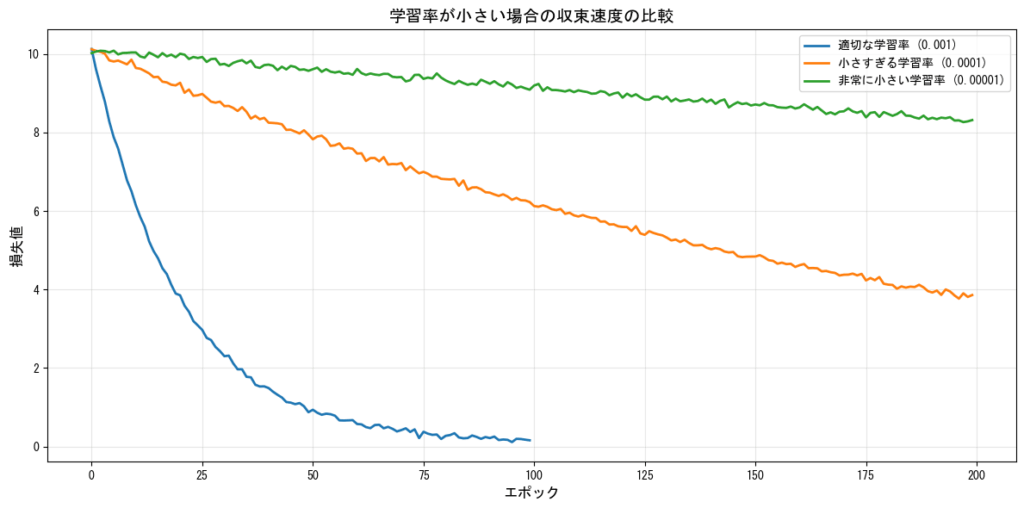
一方、学習率が小さすぎると:
- 学習の停滞:収束までに非常に長い時間がかかる
- 局所最適解への収束:悪い局所最適解から抜け出せなくなる
- 勾配消失問題の悪化:深いネットワークで特に問題となる
学習率の初期値設定
学習率の初期値は、モデルの種類やタスクによって異なりますが、一般的な推奨値があります:
| 最適化手法 | 推奨される初期学習率 | 備考 |
|---|---|---|
| SGD | 0.01 ~ 0.1 | モメンタムなしの場合 |
| SGD + Momentum | 0.001 ~ 0.01 | モメンタム付きは小さめ |
| Adam | 0.001 ~ 0.0001 | デフォルトは0.001 |
| RMSprop | 0.001 ~ 0.01 | 0.001が標準的 |
| AdaGrad | 0.01 ~ 0.1 | 自動で減衰する |
タスク別の推奨値
| タスク | 推奨される学習率範囲 | 注意点 |
|---|---|---|
| 画像分類(CNN) | 0.0001 ~ 0.001 | 事前学習済みモデルは0.0001 |
| 自然言語処理(Transformer) | 0.00001 ~ 0.0001 | ウォームアップと併用 |
| 強化学習 | 0.0001 ~ 0.001 | 環境によって大きく変動 |
| 生成モデル(GAN) | 0.0001 ~ 0.0002 | GeneratorとDiscriminatorで調整 |
学習率スケジューリング
訓練の途中で学習率を動的に変更する手法を学習率スケジューリングと呼びます。これにより、初期は大きな学習率で素早く最適解に近づき、後半は小さな学習率で精密に調整することができます。スケジューリングについては学習率スケジューラー完全ガイド:種類と実装方法 で分かりやすく解説しています。
主要なスケジューリング手法
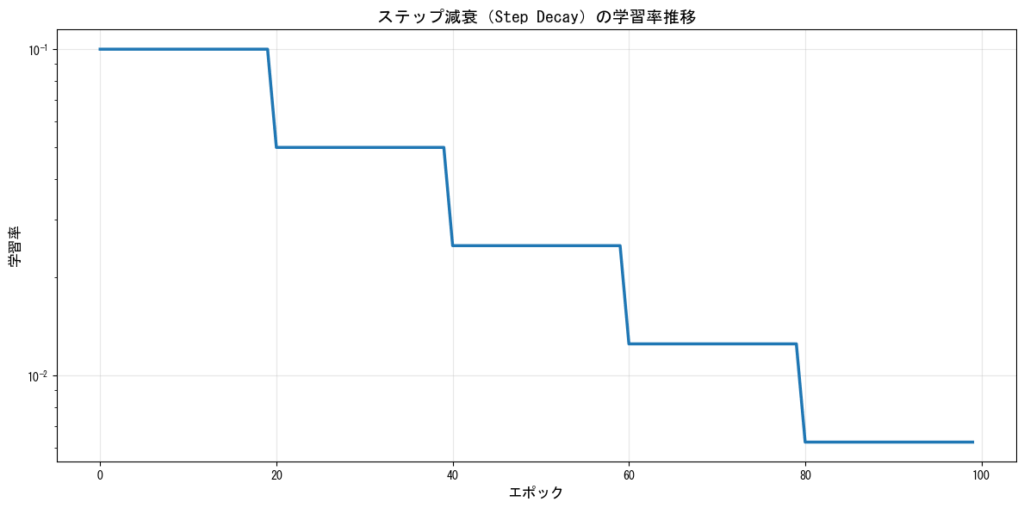
ステップ減衰(Step Decay)
一定のエポック数ごとに学習率を減少させる最もシンプルな方法です。例えば、30エポックごとに学習率を10分の1にするなどの設定が一般的です。
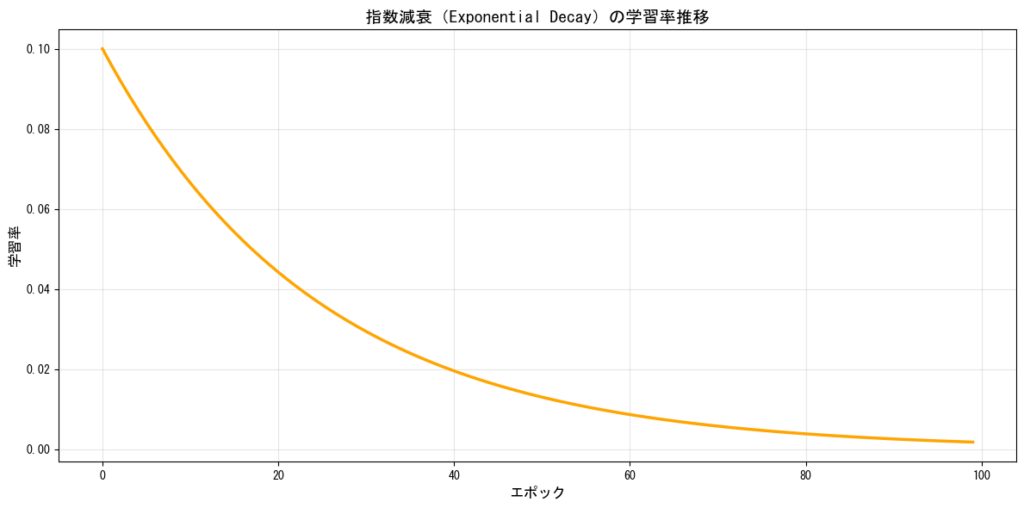
指数減衰(Exponential Decay)
学習率を指数関数的に減少させる方法です。滑らかな減衰が特徴で、多くのケースで安定した学習が可能です。
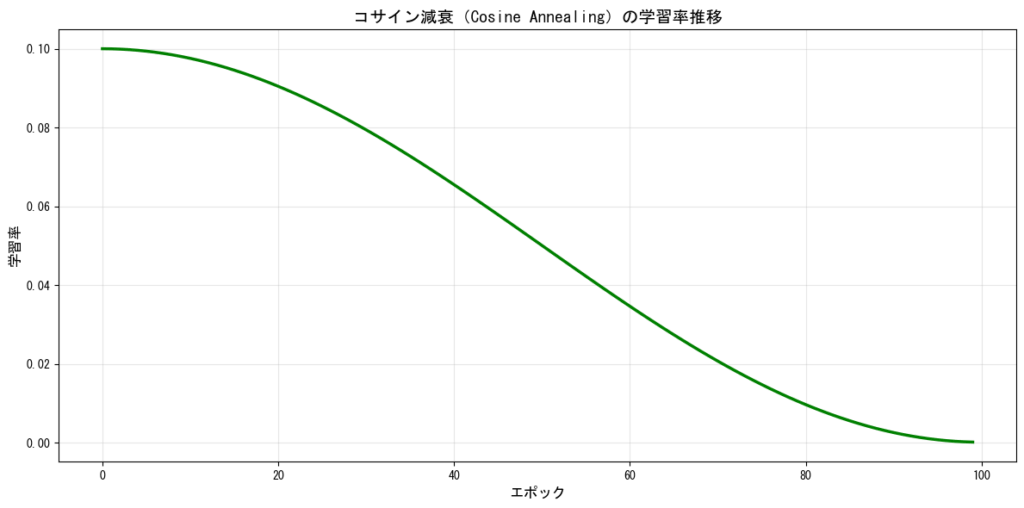
コサイン減衰(Cosine Annealing)
学習率をコサイン関数に従って減少させる方法です。ResNetなどの深層ネットワークで効果的であることが知られています。
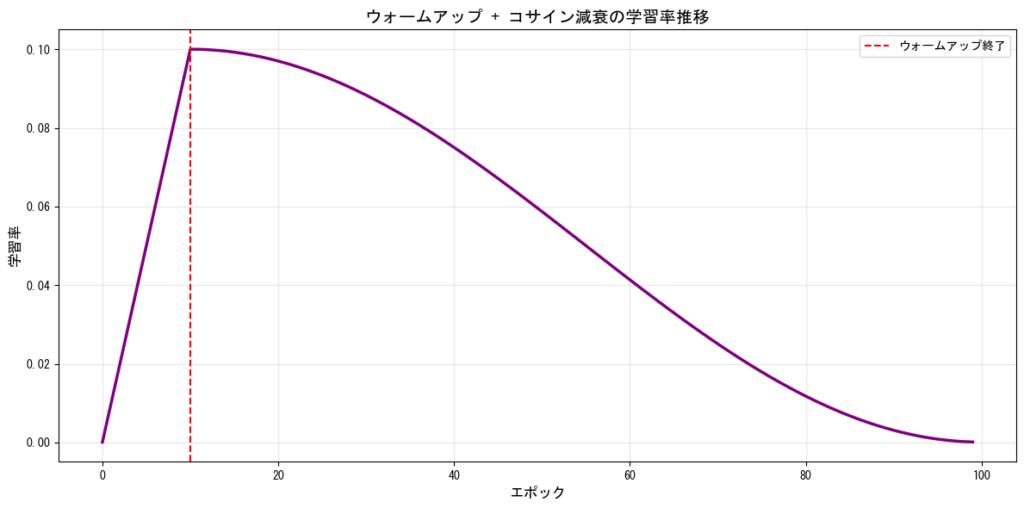
ウォームアップ(Warm-up)
訓練の初期段階で学習率を徐々に増加させる手法です。特にTransformerベースのモデルで効果的です。大規模なバッチサイズを使用する場合にも有効です。
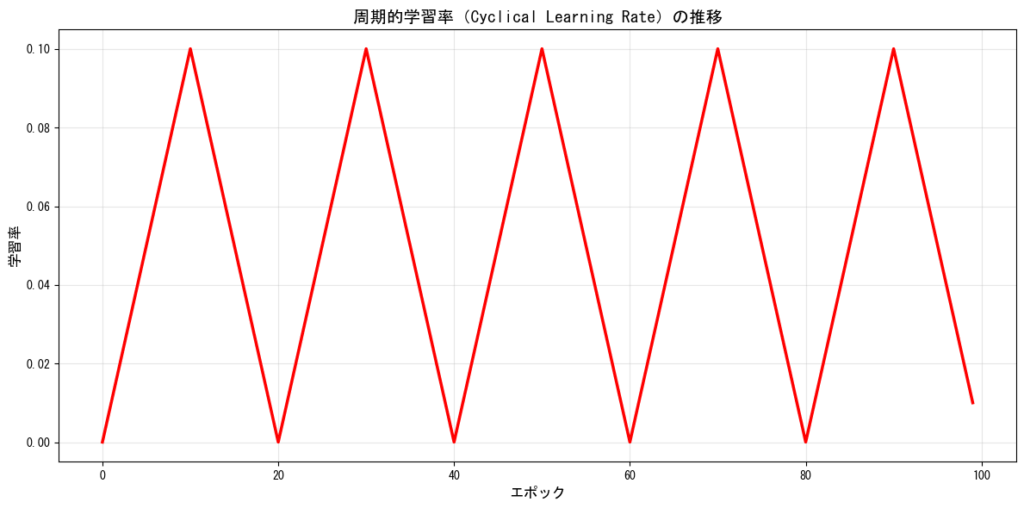
周期的学習率(Cyclical Learning Rate)
学習率を周期的に変化させる手法で、局所最適解から脱出しやすくなるという利点があります。
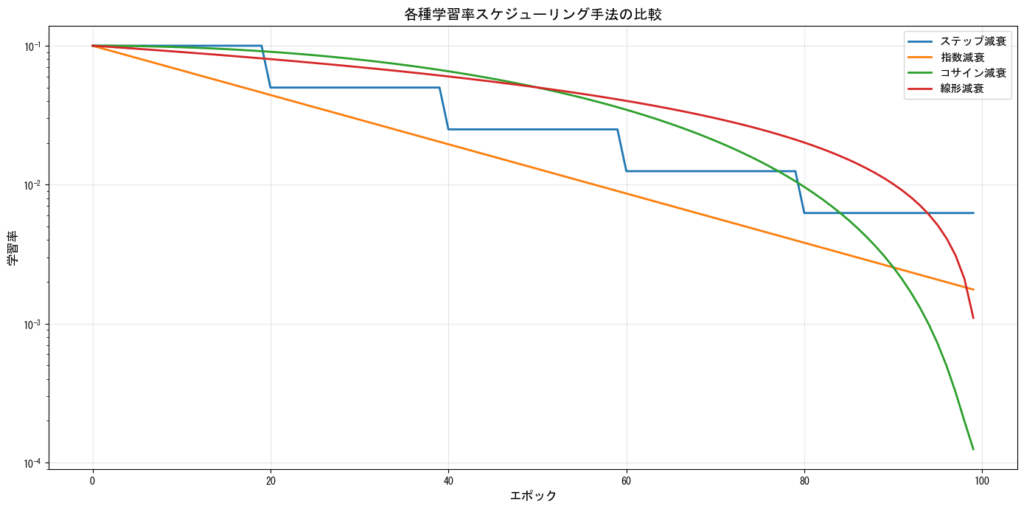
スケジューリング手法の比較
スケジューラーについて詳しくまとめている記事はこちらです。実装まで解説しています
学習率の探索方法
最適な学習率を見つけるための実践的な手法をいくつか紹介します。
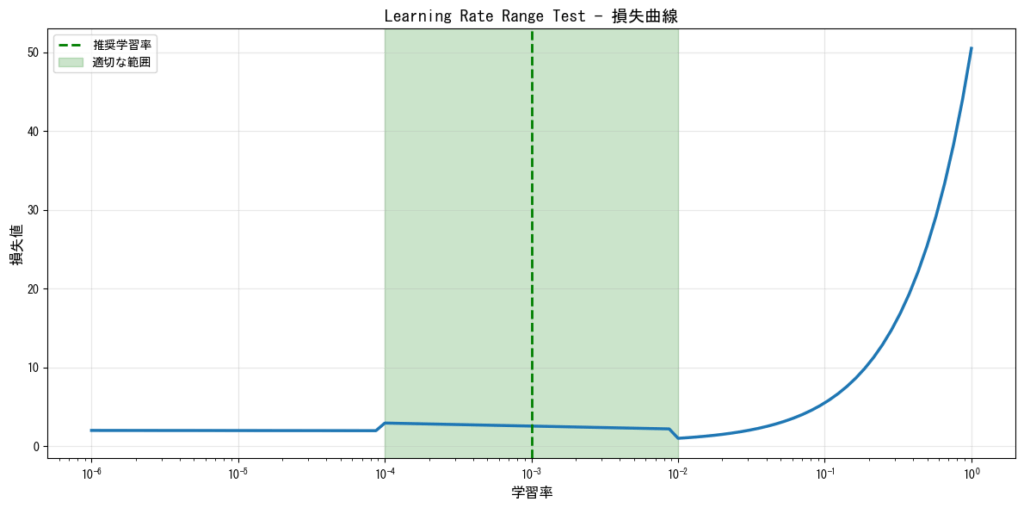
Learning Rate Range Test
Leslie Smithによって提案された手法で、学習率を徐々に増加させながら損失の変化を観察します。損失が急激に減少し始める点と、損失が発散し始める点の間が適切な学習率の範囲となります。
グリッドサーチとランダムサーチ
複数の学習率候補を試して、検証データでの性能を比較する方法です。計算コストはかかりますが、確実に良い学習率を見つけることができます。
| 手法 | 利点 | 欠点 | 推奨される場合 |
|---|---|---|---|
| グリッドサーチ | 網羅的に探索できる | 計算コストが高い | 探索空間が小さい場合 |
| ランダムサーチ | 効率的に探索できる | 最適値を見逃す可能性 | 探索空間が大きい場合 |
| ベイズ最適化 | 効率的かつ精度が高い | 実装が複雑 | 計算リソースが限られる場合 |
最適化アルゴリズムと学習率
現代の深層学習では、単純なSGDだけでなく、適応的な学習率を持つ最適化アルゴリズムが広く使用されています。
適応的学習率の最適化手法
| 手法 | 特徴 | 学習率の設定 | 主な用途 |
|---|---|---|---|
| Adam | モメンタムと適応的学習率を組み合わせ | デフォルト0.001で良好 | 汎用的に使用可能 |
| AdamW | Adamに重み減衰を改善して追加 | 0.0001~0.001 | Transformerモデル |
| RMSprop | 勾配の二乗の移動平均で正規化 | 0.001~0.01 | RNNなど |
| AdaGrad | 勾配の累積で学習率を調整 | 0.01~0.1 | スパースなデータ |
| SGD + Momentum | モメンタム項を追加したSGD | 0.01~0.1 | CNNで依然有効 |
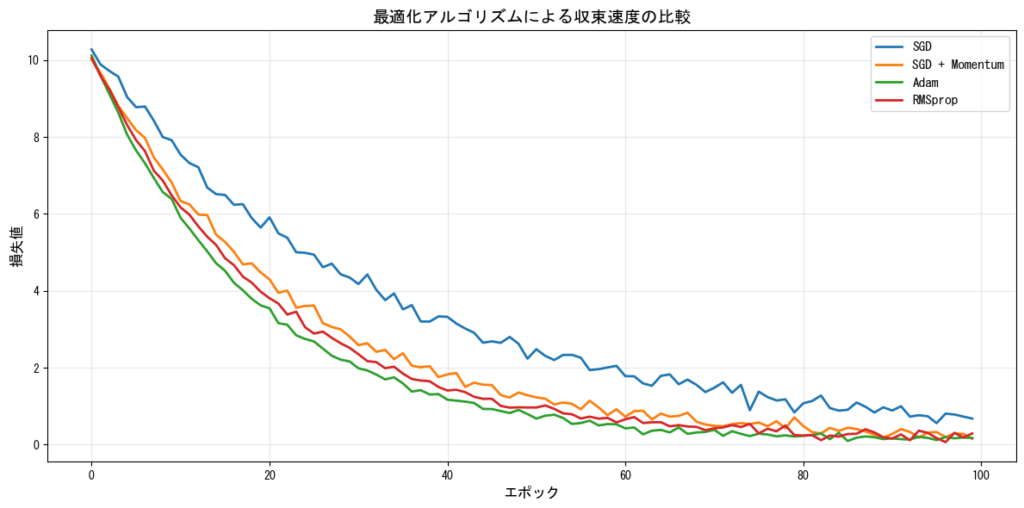
アルゴリズム別の収束特性
実践的なヒントとベストプラクティス
学習率設定のチェックリスト
- まずはデフォルト値から始める:Adamなら0.001、SGDなら0.01から試す
- 損失の推移を観察する:最初の数エポックで損失が減少しているか確認
- 学習率を段階的に調整する:10倍または10分の1ずつ変更して試す
- バッチサイズとの関係を考慮する:バッチサイズを大きくしたら学習率も増やす
- スケジューリングを併用する:固定学習率より減衰を使う方が一般的に良い
よくある問題と対処法
| 症状 | 考えられる原因 | 対処法 |
|---|---|---|
| 損失が減少しない | 学習率が小さすぎる | 10倍に増やして試す |
| 損失が発散する | 学習率が大きすぎる | 10分の1に減らす |
| 損失が振動する | 学習率が大きすぎる | 減らすか、より滑らかなスケジューリングを使う |
| 学習が途中で停滞 | 局所解に捕まった | 学習率スケジューリングを見直す |
| 検証損失が訓練損失より悪化 | 過学習 | 学習率を下げるか、正則化を強化 |
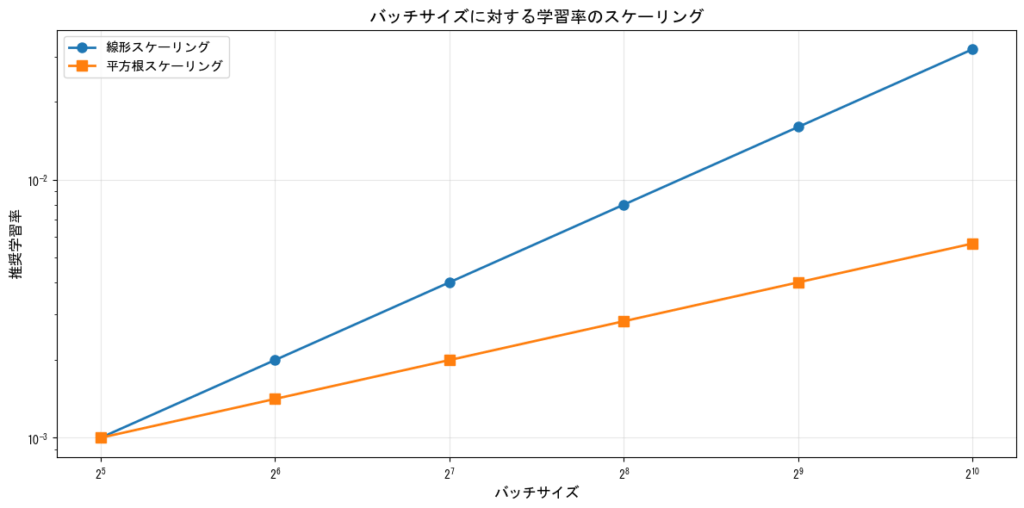
バッチサイズと学習率の関係
バッチサイズを大きくする場合、学習率も調整する必要があります。一般的な経験則として、バッチサイズをk倍にしたら学習率も√k倍または線形にk倍にすることが推奨されます。
| バッチサイズ | 推奨学習率(Adam) | 推奨学習率(SGD) |
|---|---|---|
| 32 | 0.001 | 0.01 |
| 64 | 0.0014 | 0.014 |
| 128 | 0.002 | 0.02 |
| 256 | 0.0028 | 0.028 |
| 512 | 0.004 | 0.04 |
まとめ
学習率は深層学習において最も重要なハイパーパラメータの一つです。適切な学習率の設定と調整により、モデルの訓練を効率化し、より良い性能を引き出すことができます。
重要なポイントをまとめると:
- 初期値は標準的な値から始める:Adam(0.001)、SGD(0.01)など
- 学習率スケジューリングを活用する:固定値よりも減衰を使う方が効果的
- Learning Rate Range Testで探索する:最適な学習率の範囲を科学的に見つける
- 最適化アルゴリズムを適切に選択する:タスクに応じてAdamやSGDを使い分ける
- バッチサイズとの関係を考慮する:バッチサイズを変更したら学習率も調整
学習率の調整は経験と実験が必要ですが、本記事で紹介した原則とテクニックを活用することで、より効率的にモデルを訓練できるようになるでしょう。自分のタスクに最適な学習率を見つけるために、様々な設定を試してみてください。



コメント